Why complex functions are amazing

A primer into complex analysis!

One of my favorite subjects in undergrad was complex analysis.

Some pictures of complex functions (aren't they pretty?)

While real analysis felt technical and unwieldy, complex analysis felt pristine. All the proofs were short and elegant. The theorem statements were clean and powerful.

But out of all the theorems I learned in complex analysis, three of them stuck in my mind. I want to share them with you.

Fact #1: once differentiable means infinitely differentiable

If a complex function is differentiable once, it is differentiable infinitely many times.

This is completely false in real analysis.

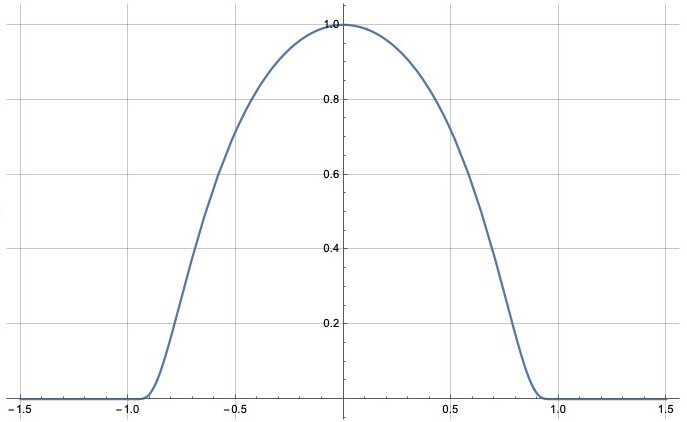
There are many functions which are differentiable once but not twice. An example of such a function is

\(f(x) = x^2 \sin(1/x)\)

at the origin (where we set f(0) = 0). See the picture below.

This function is differentiable once (but not twice!) at the origin.

This is never the case in the complex world.

Fact #2: Liouville’s Theorem

If a complex differentiable function on the complex plane is bounded, it is constant.

This is incredibly startling!

And it is completely false for real functions — for example, sin(x) is bounded and non-constant.

But the complex sine function (pictured below) is in fact unbounded in the imaginary axis of the complex plane!

The complex sine is unbounded in the complex plane.

Fact #3: Identity Theorem

If a complex differentiable function on the complex plane is zero on an open subset of the complex plane, it is zero everywhere.

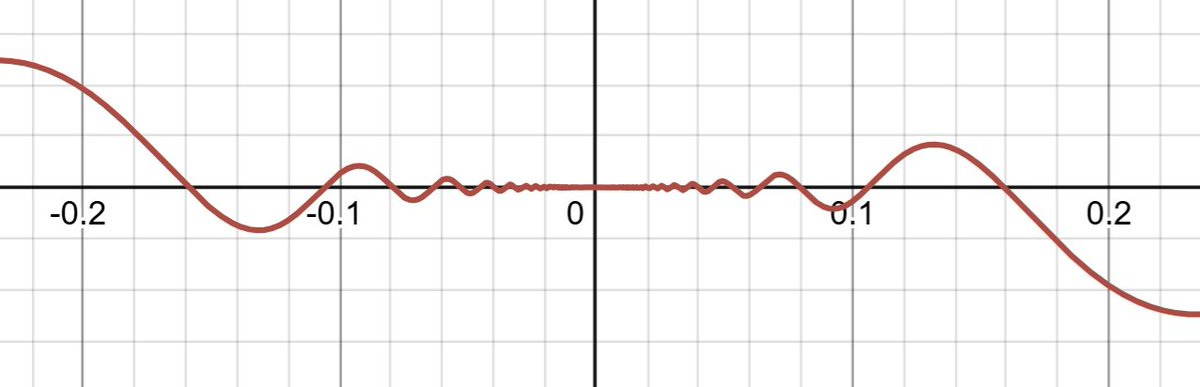
Again, this is totally false for real functions. There many smooth real functions which are zero on an open interval but not zero everywhere, e.g: the graph below.

This function is zero outside (-1,1), but not identically zero.

Problem of the week

Here is the challenge problem for this week:

Prove that if x,y,z are real numbers from [0,1], then

\(2(x^3 + y^3 + z^3) - x^2y - y^2z - z^2x \leq 3.\)

Got a solution to the challenge problem? Submit it here.

Thanks for reading and happy learning! Until next time,

Adithya