The world's hardest math problem

... and why it may not be as hard as we think

I was flipping through my old files and I found this flyer from an old conference.

It was a 3-day conference in analytic number theory at the Fields Institute.

A lot of the talks there were about the Riemann Hypothesis, one of the biggest open problems in number theory.

I learned something very surprising: there has actually been quite a lot of progress towards the Riemann Hypothesis!

But for some reason, this recent progress is only known among specialists.

So in this issue, I wanted to disseminate this information more widely. (Who knows, maybe one of you could make your own contributions!)

But first, what is the Riemann Hypothesis?

The Riemann Hypothesis (RH) is a famous unsolved problem in number theory. Since there are many wonderful explanations of this problem online, I’ll give a “cliff-notes” explanation.

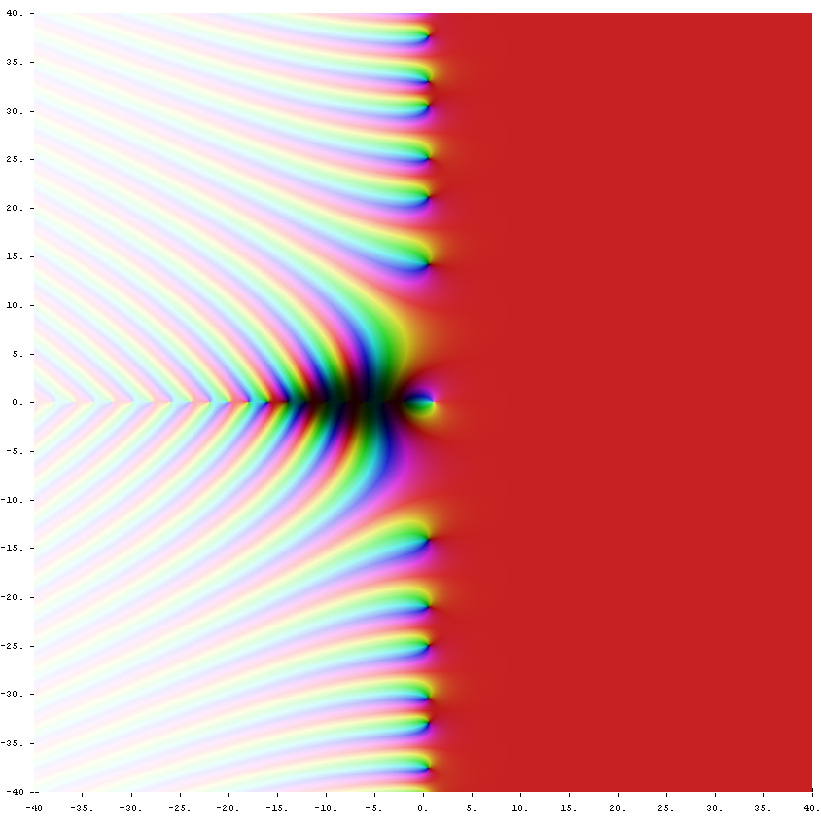
The main character in RH is the Riemann zeta function, which is defined as follows:

\(\zeta(s) = \dfrac{1}{1^s} + \dfrac{1}{2^s} + \dfrac{1}{3^s} + \dots.\)

Here are some quick facts about this function.

1. The zeta function converges for complex numbers s with Re(s) > 1.

2. The zeta function can be “analytically continued” so that it is defined on the entire complex plane.

3. The zeta function vanishes at all negative even integers; that is:

\(\zeta(s) = 0 \text{ for }s=-2,-4,-6, \dots\)

These are called the “trivial zeroes” of the zeta function.

The famous (and still unproven) Riemann Hypothesis asserts:

All the zeroes of the zeta function (other than the trivial zeroes) lie on the line Re(s)=1/2.

A graph of the zeta function near the critical line.

The Clay Math Institute has offered a million-dollar prize for anyone who can prove or disprove this conjecture.

Should we try solving it?

The general consensus among experts seems to be that RH is simply beyond the reach of what mathematics can prove at the moment.

That being said, most open problems seem impossible until they are solved. Fermat’s Last Theorem is a prime example. Everyone thought it was inaccessible to current methods until Wiles came along and solved it. So who knows?

What progress have we made?

It turns out: there has been a lot of very strong progress towards the Riemann Hypothesis in the past century. Here are some examples.

It is now known that a positive proportion of non-trivial zeta zeroes are on the critical line. Here is a timeline of the progress made:

1. As early as 1942, Atle Selberg proved using an ingenious method that a positive proportion of the nontrivial zeros are on the critical line. (“Positive proportion” means “more than 0%”.) To do this, Selberg developed a tool called the mollifier method.

2. In 1974, in a beautiful paper, Norman Levinson combined the mollifier method with several new innovations. The result: more than one third of the non-trivial zeta zeroes are on the critical line.

3. In 1989, John Brian Conrey showed that at least two-fifth of the zeta zeroes are on the critical line. To do this, Conrey used deep techniques involving objects called Kloosterman sums.

Selberg, Levinson, Conrey (left to right)

Is this enough to prove RH?

Definitely not. Even if we can show that 100% of zeta zeroes are on the critical line, that will not imply the Riemann Hypothesis! The phrase “100%” is asymptotic, whereas RH says that every single zeta zero is on the critical line.

That being said, maybe the techniques in the proofs can shed some light on what is needed to prove or disprove RH in general.

Challenge Problem

As always, here is a challenge problem for this week:

Find all positive solutions of the system of equations

\(\begin{align*} x_1 + x_2 &= x_3^2 \\ x_2 + x_3 &= x_4^2 \\ x_3 + x_4 &= x_5^2 \\ x_4 + x_5 &= x_1^2 \\ x_5 + x_1 &= x_2^2. \end{align*}\)

If you have a solution to this problem, submit it here for a chance to be featured in the next issue of this newsletter.

Feedback

If you have any learning resources that you think would be valuable for readers, or if you have any general feedback, let me know here (or just reply to this email) and I’d be happy to incorporate it.

Thanks for reading and happy learning! Until next time,

Adithya