The prime number theorem, explained

+ a cute geometry puzzle

One of my favorite theorems is the Prime Number Theorem.

To motivative it, let’s start with an easier question:

How many primes are there?

Alright, this is an easy question to answer. It’s been known since ancient times that there are infinitely many primes.

But I’m really asking a more quantitative question: how many primes are there, quantitatively speaking?

Here’s a good place to start. It's a famous fact that the sums of reciprocals of squares converges:

\(\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+⋯<∞.\)

However, the sum of reciprocals of the primes diverges!

\(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}+⋯=∞.\)

This means, heuristically speaking:

There are “more” primes than squares.

How does this help us?

The number of squares less than X is (approximately) the square root of X. So we would expect the number of primes less than X to be (roughly) more than the square root of X.

This is already a non-obvious fact about primes.

Enter: analytic number theory

The above heuristic discussion gave us a start: the number of primes less than X is “more than” the sqrt(X).

This gives us a lower bound. But what is the answer exactly?

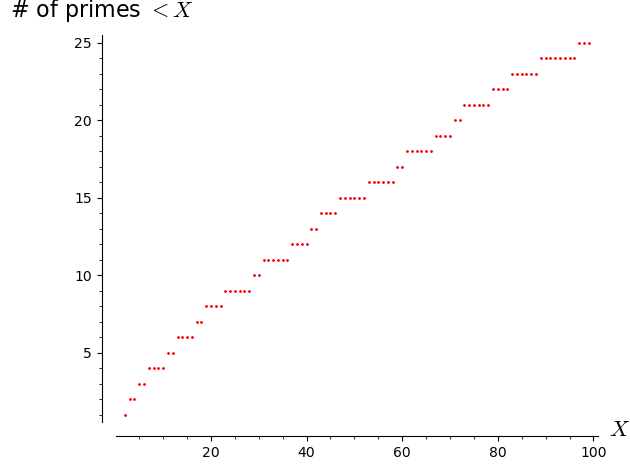
This question is very hard to answer because the primes are chaotically distributed. The prime counting function is hard to predict. Here’s a graph:

It seems to grow somewhat steadily but it is not a straight line.

The Prime Number Theorem (PNT) gives a good approximation for how this function grows.

What is the Prime Number Theorem?

Roughly, the Prime Number Theorem (PNT) says that if X is large, roughly X / log X of the integers less than X are prime.

Precisely, the PNT says:

\(\{\# \text{of primes less than }X\}∼X/\log⁡X.\)

This squiggle means "asymptotic to". It’s defined as follows.

\(f(X)∼g(X) \text{ means } \lim_{X→∞} f(X)/g(X)=1.\)

In other words, define the prime counting function as follows:

\(\pi(X)= \# \text{ of primes less than }X\)

The PNT says that

\(π(X)/(X/\log ⁡X) \to 1 \quad \text{as} \quad X \to \infty.\)

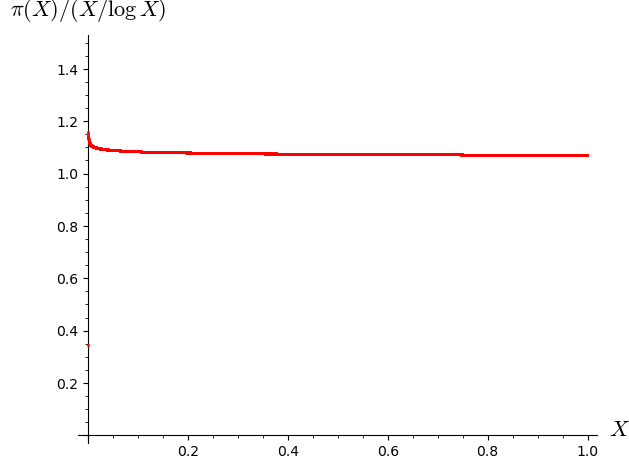
Here is a graph of this function:

This function goes to 1 as X gets larger. (But as you can see, it converges very slowly!)

Problem of the Week

Here is the challenge problem for this week:

The vertices and midpoints of the faces are marked on a cube, and all face diagonals are drawn. Is it possible to visit all marked points by walking along the face diagonals?

Got a solution to the challenge problem? Submit it here.

Solution from last week

See here for the solution. (Shoutout to Bethany from Texas whose solution is being featured this week!)

Huge thanks to Joan Llobera (Lleida, Catalonia), Mark Spindler (Maryland), Ibrahim (California), Kurt Wynn (Brockton Bay), David J. Webb (Hawaii), Darko L (Serbia), Martin Masson (France), Bethany (Texas), jc (New York), and Aayush Rath (India) for submitting solutions to this challenge problem.

Thanks for reading and happy learning! Until next time,

Adithya