Math in higher dimensions: homology & manifolds

+ an intriguing calculus problem!

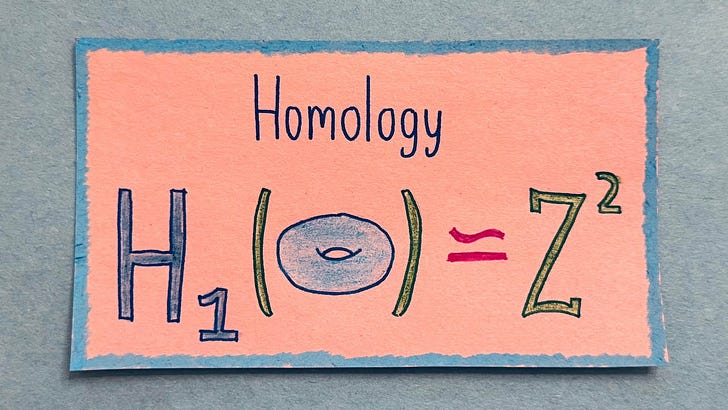
Homology, explained

I recently made a new video about algebraic topology, specifically homology. This is the mathematical study of how to rigorously define what it means for a space to have “holes”.

Check it out here:

Manifolds, explained

A core concept in differential geometry is that of a manifold. Roughly speaking, a manifold is a generalization of curves and surfaces to arbitrary dimensions.

I couldn’t explain manifolds better than mathematician John Lee, who writes:

Mathematicians have developed a wondrous collection of conceptual machines that enable us to peer ever more deeply into the invisible world of geometry in higher dimensions. Once their operation is mastered, these powerful machines enable us to think geometrically about the 6-dimensional solution set of a polynomial equation in four complex variables, or the 10-dimensional manifold of 5-by-5 orthogonal matrices, as easily as we think about the familiar 2-dimensional sphere in R³.

In short, manifolds allow you to do geometry in higher-dimensions.

However, the definition of a manifold is formidable. It took a while for me to understand the intuition behind it.

So I wanted to share a brief explanation here:

(The quote above is from the introduction to Lee’s wonderful book, Introduction to Smooth Manifolds, which I highly recommend reading.)

Problem of the Week

Define a sequence {x_n} as follows:

\(x_0 = 0, \hspace{20pt} x_{n+1} = \sqrt{4 + 3x_n}.\)

Show that this sequence is convergent and find its limit.

If you have a solution to the above challenge problem, submit it here for a chance to be featured in the next issue of this newsletter.

Solution from last week

See here for the solution to last week’s problem. (Shoutout to Daniel Holst (Sweden) whose solution is being featured this week!)

Huge thanks to Subhadeep Pal, Bangalore (India), Daniel Holst (Sweden), Jorge Solloa (Mexico City), Anthony (California), B Sashi Kanth (Hyderabad, India), jc (New York), Han Geurdes (Netherlands), and Han Geurdes for submitting solutions to last week’s challenge problem.

Thanks for reading! See you next week,

Adithya

Share and subscribe!
YouTube: https://www.youtube.com/@Aleph0
Twitter: https://x.com/00aleph00