An exciting result in the world of elliptic curves!

A recent finding of an elliptic curve with rank at least 29!

A quick question for you!

Are you struggling with career stagnation and job insecurity due to insufficient advanced math skills?

If this is you, I’d love to ask you few questions about your experience. This is in preparation for a program I’m building to help working professionals in math-heavy careers, and it’s purely for my own research.

If you're open to chatting, please fill out this form here. Thanks in advance!

A recent breakthrough about elliptic curves

Now let’s get into the math.

Mathematicians Elkies and Klagsbrun have recently announced the following result:

There exists an elliptic curve over the rationals with rank at least 29.

This breaks a previous record which was established by Elkies in 2006 of an elliptic curve with rank at least 28.

In this issue, I’d like to explain what this result is.

What are elliptic curves?

An elliptic curve is a curves of the following form:

\(y^2=x^3+Ax+B\)

where A and B are constants. The fundamental question that mathematicians want to understand about elliptic curves is:

How many rational solutions does this curve have?

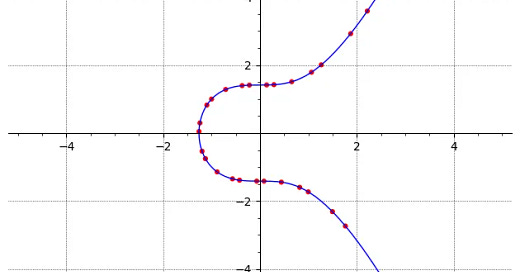
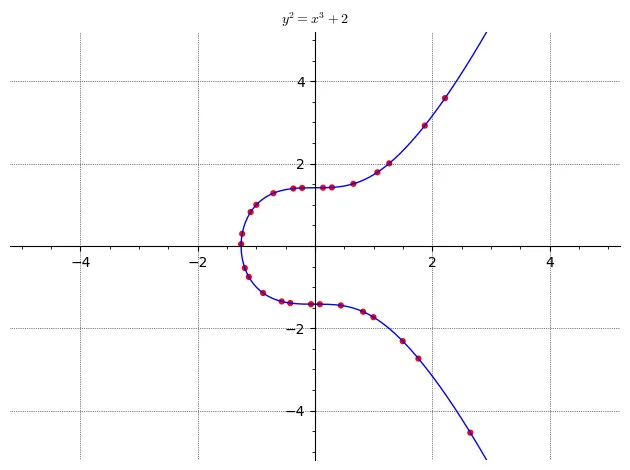
For example, below I’ve highlighted the rational solutions to this elliptic curve as red dots. This curve below has infinitely many rational points.

The group law on an elliptic curve

In the 1900s, Poincare figured out a neat trick to generate new rational points on an elliptic curve. Here’s how it goes:

1. Suppose you have two rational points P and Q on the elliptic curve. Connect them with a line.

2. That line will intersect the elliptic curve at a third point. Call that third point R.

3. Now reflect R across the x-axis. Call that point P+Q.

If P and Q are rational points, then the sum P+Q (defined as above) will also be a rational point. This 3-step process is called the chord-and-tangent process. Given two rational points P and Q, this gives a way to combine them to produce a third point, which we denote P+Q.

The rank of an elliptic curve

Given an elliptic curve E, we let E(Q) denote the set of all rational points on E. Here are three elliptic curves, along with the set of rational points:

Example 1:

\(\begin{align*} E: y^2 = & x^3 - 2 \\ E(\mathbb{Q}) = \{ n &\cdot (3,5) : n \in \mathbb{Z} \} \end{align*}\)

Example 2:

\(\begin{align*} E: y^2 = x^3 - &3024x + 46224 \\ E(\mathbb{Q}) = \{ n \cdot (-24, 324) + &m \cdot (12, 108): m,n \in \mathbb{Z} \} \end{align*}\)

Example 3:

\(\begin{align*} &E: y^2 = x^3 - x\\ &E(\mathbb{Q}) \text{ is finite!} \end{align*}\)

The rank of an elliptic curve is the “number of copies of the integers” in E(Q). So:

1. The first curve has rank 1 since there is one copy of the integers in E(Q).

2. The second curve has rank 2 since there are two copies of the integers in E(Q).

3. The last curve has rank 0 since E(Q) is finite.

How big can the rank get?

Here is a recent chronology of “rank records” of elliptic curves over the rationals.

• In 1938, Billing produced an elliptic curve of rank at least 3.

• In 1982, Mestre produced an elliptic curve of rank at least 12.

• In 1993, Nagao produced an elliptic curve of rank at least 20.

• In 2006, Elkies produced an elliptic curve of rank at least 28.

(This is just a sample of the rank results. If you’re curious, you can see the full table here.)

And now — 18 years later — Elkies and Klagsbrun have broken this record after 18-years, producing an elliptic curve of rank at least 29. They’ve explicitly written down the equation for the curve and produced 29 independent points of infinite order.

It is a wide open question whether there are elliptic curves over the rationals with arbitrarily large rank.

Problem of the Week

Here is this week’s challenge problem:

Prove that if you add up the reciprocals of a sequence of consecutive positive integers, the numerator of the sum (in lowest terms) will always be odd. For example,

\(\dfrac{1}{7} + \dfrac{1}{8} + \dfrac{1}{9} = \dfrac{191}{504}.\)

If you have a solution to this problem, submit it here for a chance to be featured in the next issue of this newsletter.

Thanks for reading and happy learning! Until next time,

Adithya